Đồ thị tính toán là gì? luồng gradient là gì

Đồ thị tính toán là gì? 

Như colah đã nói khá hay: đồ thị tính toán là một cách hay để suy nghĩ về các biểu thức toán học.

Ví dụ,  hãy xem xét biểu thức: e=(a+b)∗(b+1)

$$\begin{gathered} c=f1(a,b)=(a+b) \\ d=f2\left(b\right)=(b+1) \\ e=f3(c,d)=(c\ast d) \end{gathered}$$

Để tạo một biểu đồ tính toán, chúng tôi thực hiện từng thao tác này, cùng với các biến đầu vào, thành các nút. Khi giá trị của một nút là đầu vào cho nút khác, một mũi tên sẽ đi từ nút này sang nút khác.

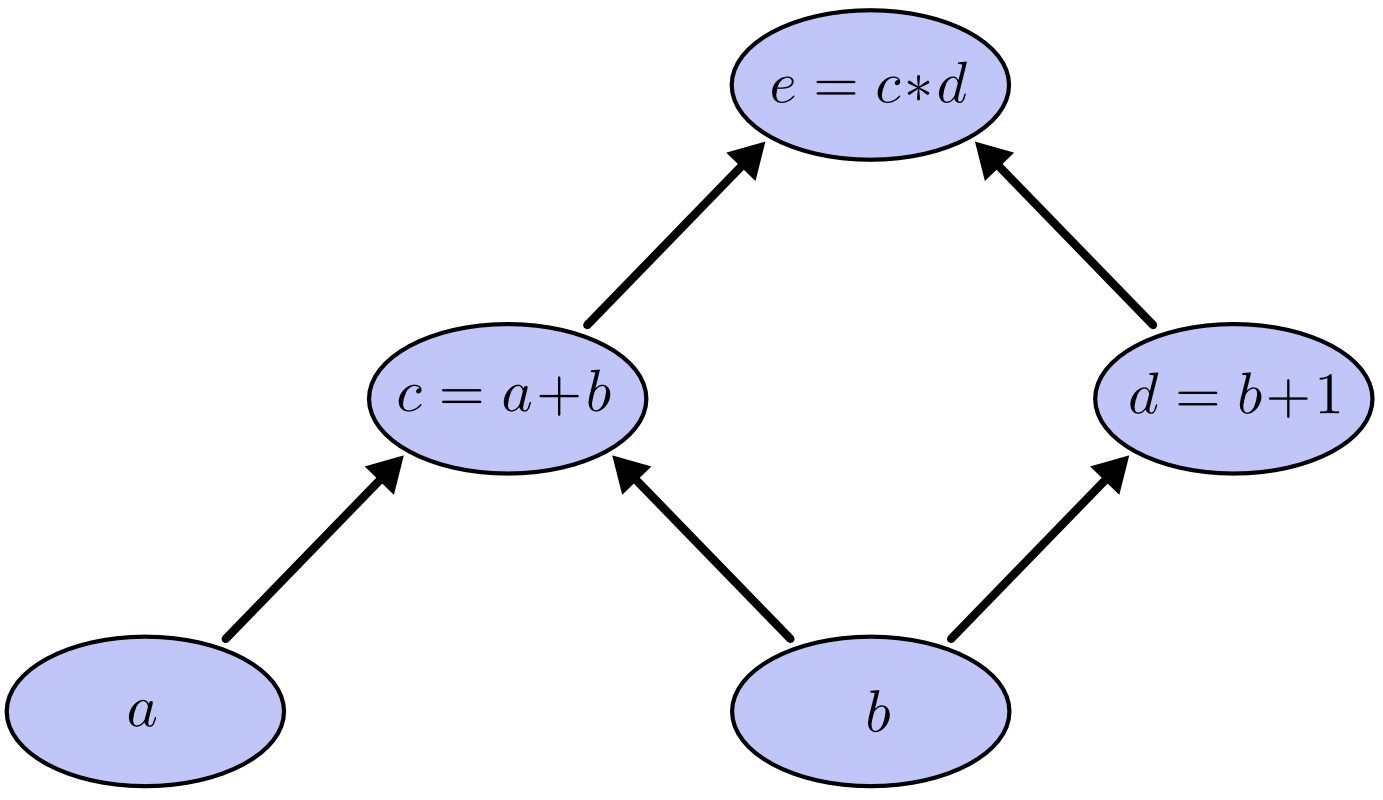
Chúng ta có thể đánh giá biểu thức bằng cách đặt các biến đầu vào (tức là các nút chỉ có đầu ra) thành các giá trị nhất định và tính toán các nút thông qua biểu đồ.

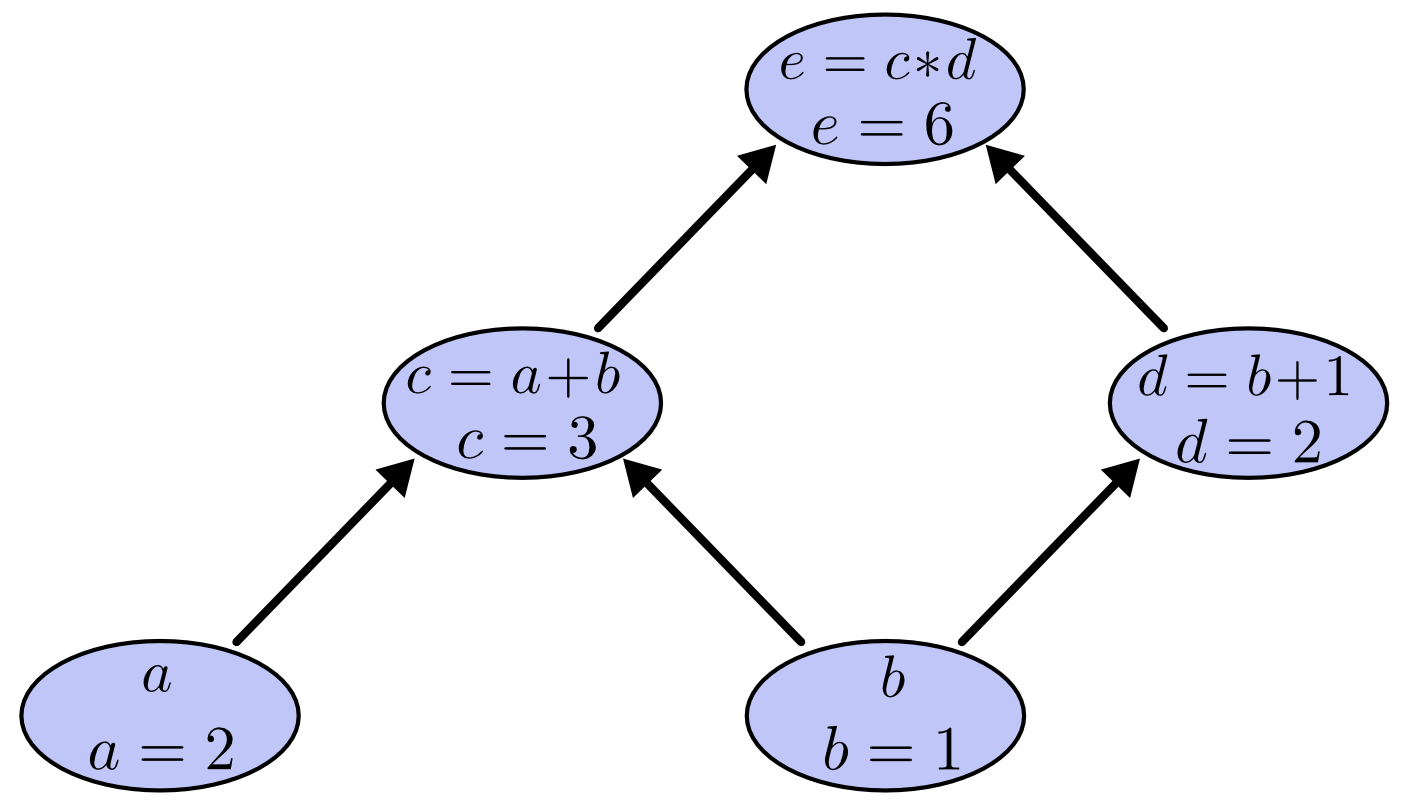
Trong ví dụ dưới đây, nếu chúng ta đạt a=2, và b=1 chúng tôi nhận được đầu ra e=6

Đạo hàm trên đồ thị tính toán

Đạo hàm (còn gọi là gradient) trên đồ thị tính toán khó hiểu hơn một chút. Tôi sẽ đi chệch khỏi lời giải thích của Colah và cung cấp nhiều ví dụ rõ ràng hơn hướng đến mạng lưới thần kinh.

Bạn được khuyến khích làm việc thông qua các ví dụ sau mà không cần nhìn vào câu trả lời ngay lập tức. Mỗi lần mất khoảng 5 phút sử dụng bút và giấy.

Ví dụ: Biểu đồ tính toán toàn diện

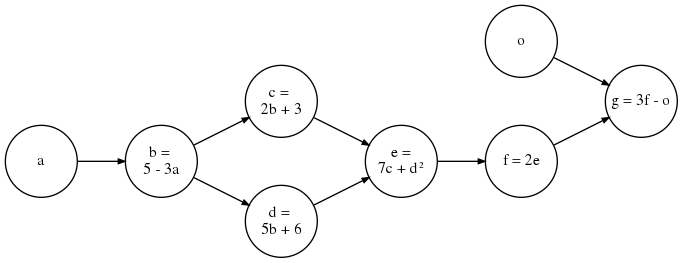
Hãy xem xét biểu đồ trên. Ở đây, đầu ra là g=3f−o và mỗi nút tính toán một hàm đầu vào của chúng, sau đó được chuyển cho (các) nút tiếp theo.

Bây giờ, giả sử chúng ta muốn tính đạo hàm riêng tức là độ dốc của đầu ra g, đối với từng biến, tức là chúng tôi muốn biết:$\frac{\partial g}{\partial g} , \frac{\partial g}{\partial o} ,\frac{\partial g}{\partial f} ,\frac{\partial g}{\partial e} ,\frac{\partial g}{\partial d} ,\frac{\partial g}{\partial c} ,\frac{\partial g}{\partial b} ,\frac{\partial g}{\partial a}$

Một vài điều đầu tiên rất dễ dàng:

Tuy nhiên, khi chúng ta tiến xa hơn về phía đầu vào của biểu đồ, mọi chuyện sẽ trở nên phức tạp hơn:

Nếu quy trình trên có vẻ quen thuộc với lập trình động, thì đó là vì nó chính xác là như vậy!

Chúng tôi lưu trữ đạo hàm riêng (còn gọi là “độ dốc”) mà chúng tôi đã tính toán trước đó và sử dụng chúng để tính các giá trị độ dốc tiếp theo.

Lưu ý rằng chúng ta chỉ có thể làm như vậy khi di chuyển từ đầu ra sang đầu vào của biểu đồ, tức là “ngược” so với luồng dữ liệu thông thường.

Hãy tiếp tục với ví dụ của chúng tôi và tính giá trị của ∂𝑔/∂𝑏. Nhưng nếu chúng ta nhìn vào sơ đồ, 𝑏 nạp vào cả hai 𝑐 Và 𝑑 …chúng ta chọn giá trị nào làm giá trị “được tính toán trước”?

Câu trả lời là: cả hai . Trong tình huống này, chúng ta phải sử dụng phần mở rộng của quy tắc chuỗi thông thường, được gọi là quy tắc Chuỗi đa biến (với một biến đầu vào duy nhất) .

Theo quy tắc chuỗi nhiều biến, để lấy đạo hàm riêng của 𝑔 liên quan đến 𝑏, chúng ta phải lấy tổng tích của các gradient dọc theo tất cả các đường đi có thể, truy ngược từ 𝑔  ĐẾN 𝑏.